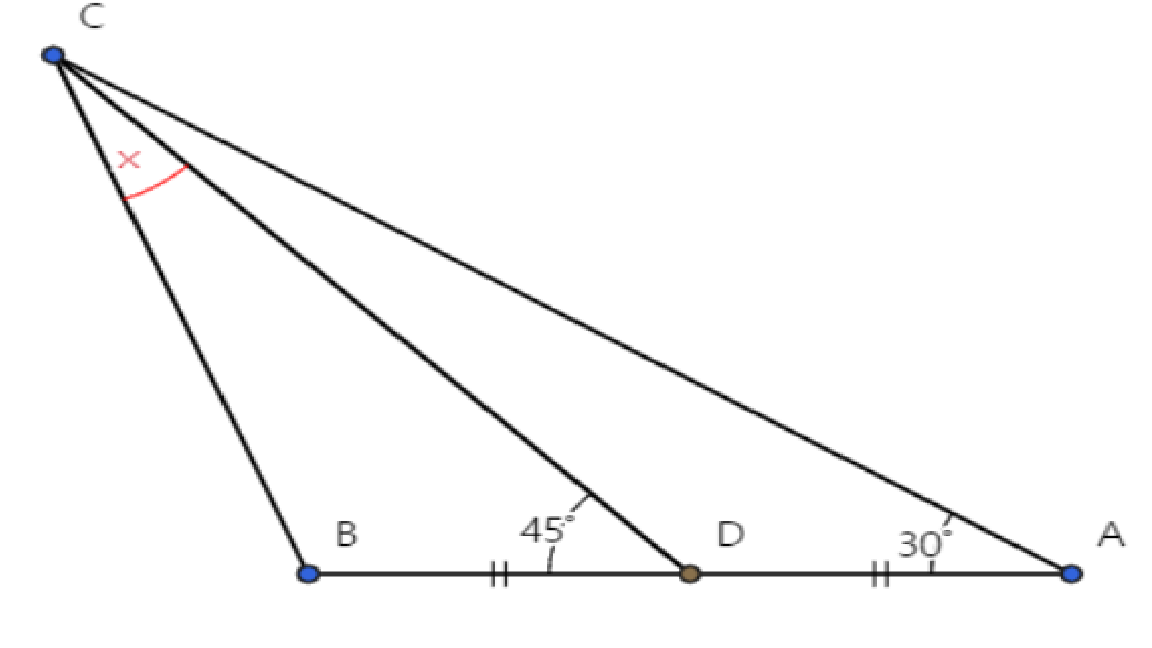
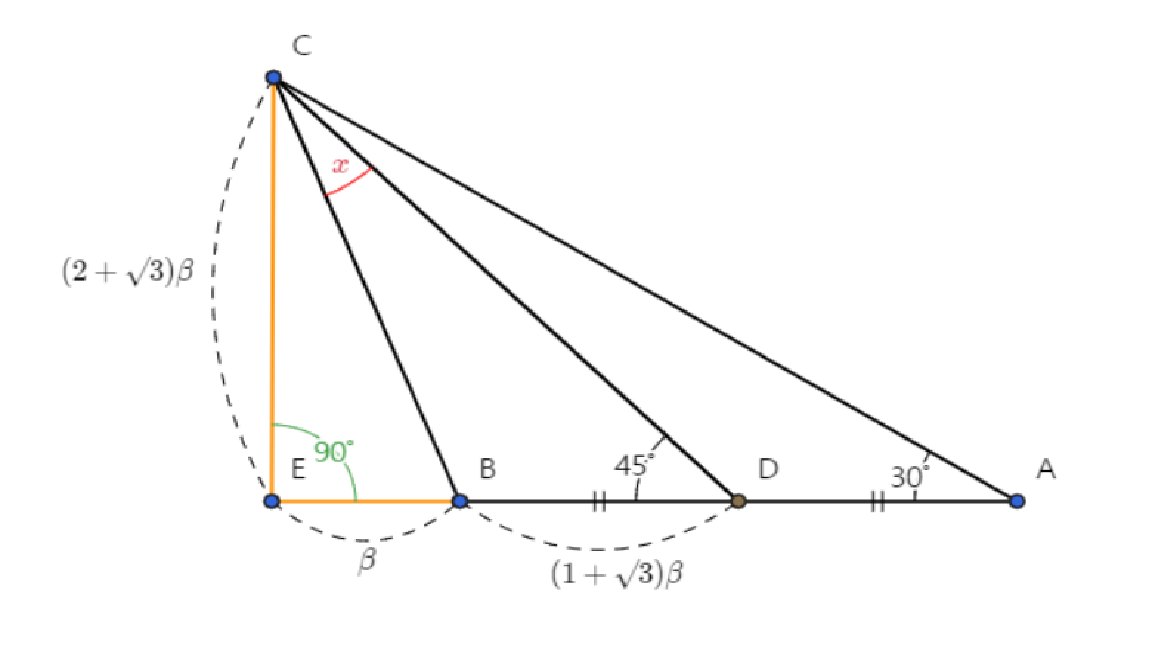
선분 AB에서 90º에서 점 C에서 떨어지는 점을 E라고 합니다.
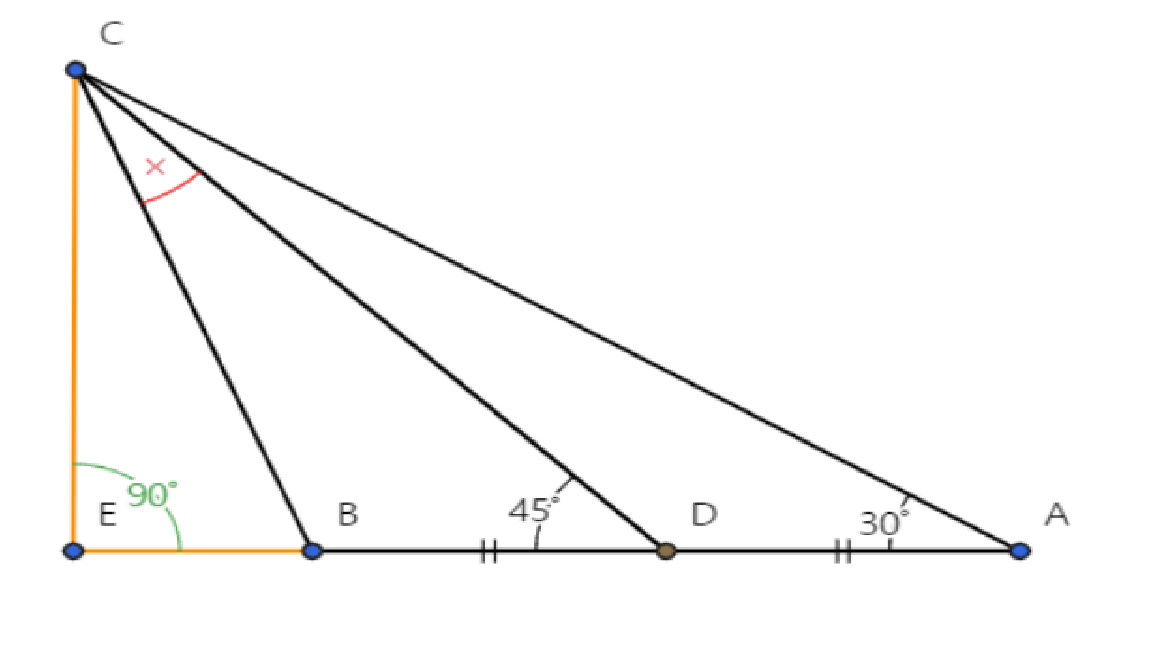
AD = α 및 BE = β라고 하자.
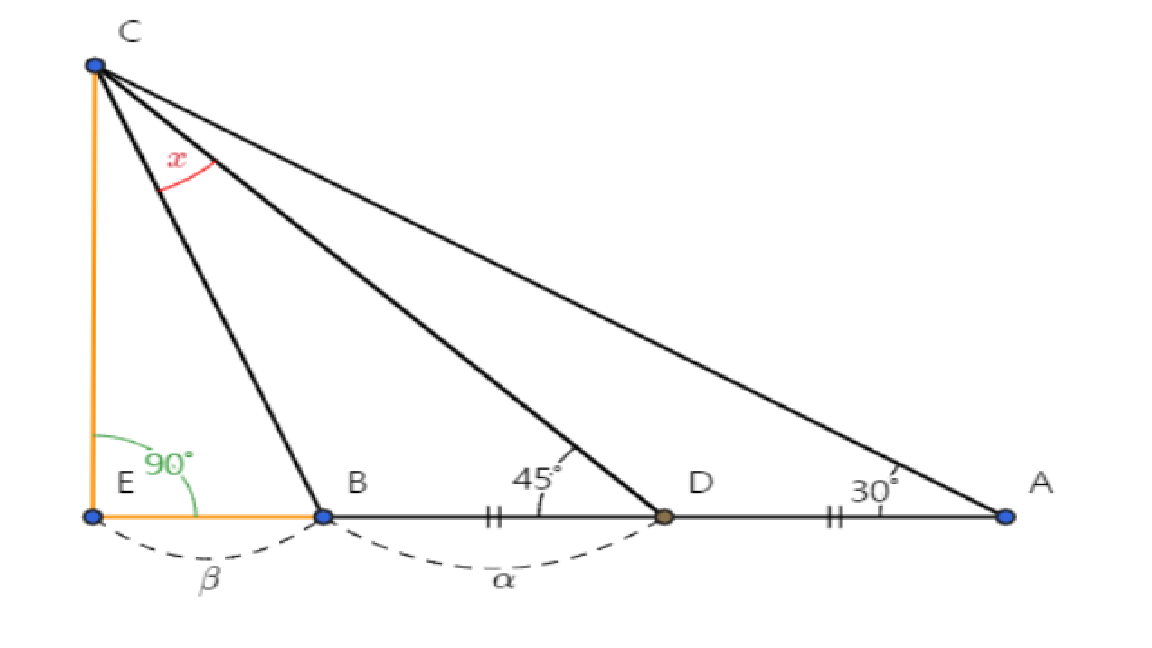
ΔCDE는 직각 이등변 삼각형이므로 CE = DE
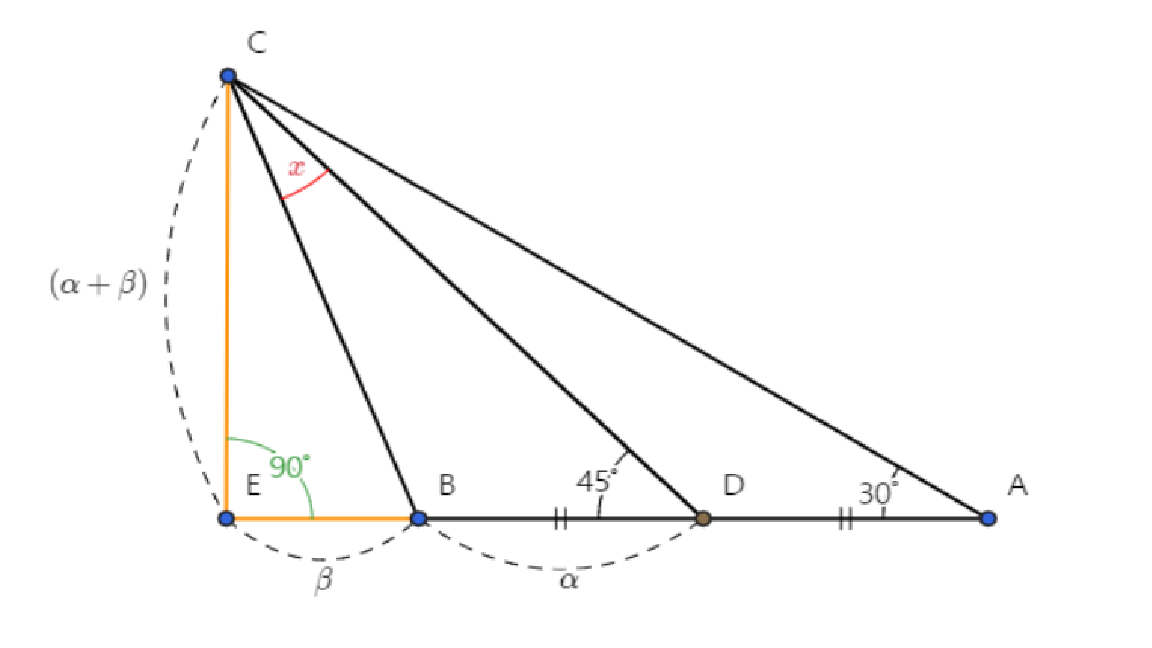
ΔACE to tan(∠CAE) = CE / AE
tan(∠CAE) = (α+β) / (2α+β) ,(∠CAE = 30º)
tan30º = (α+β) / (2α+β) ,(tan30º = 1/√3)
1/√3 = (α+β) / (2α+β)
(2α+β) = √3α + √3β
(2-√3)α = (√3-1)β ,{양변에 (2+√3)을 곱함}
α = (2+√3)(√3-1)베타
α = (1+√3)β
ΔCDE는 직각 이등변 삼각형이므로 ∠DCE = 45º
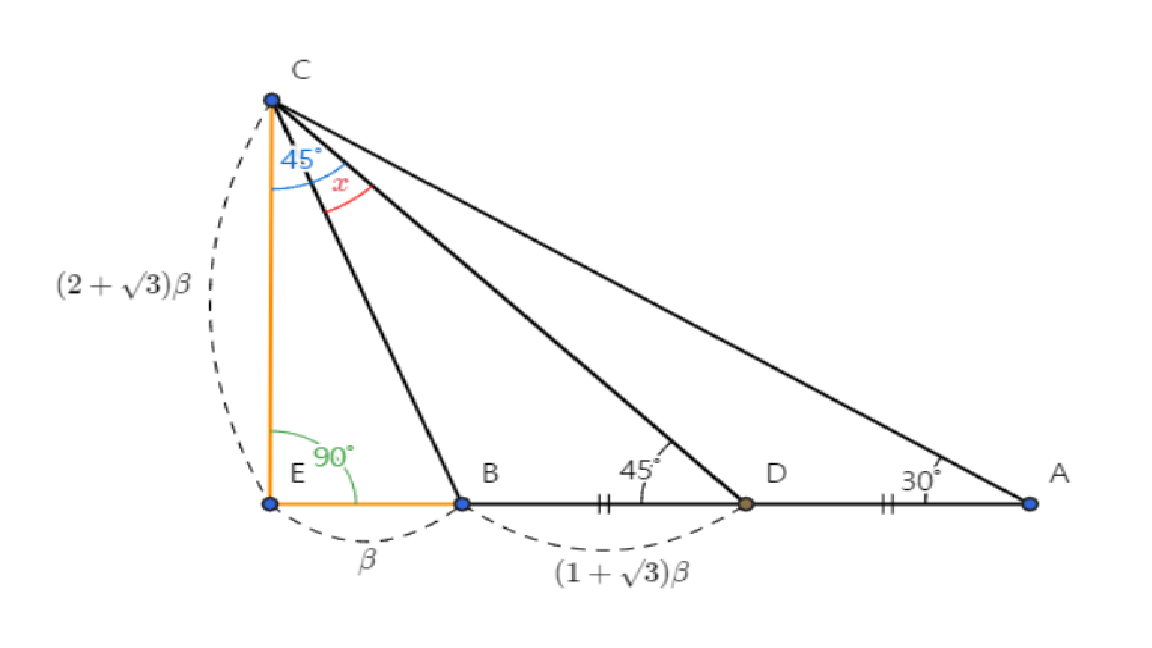
ΔCEB to tan(∠BCE) = BE / CE
tan(∠BCE) = β / (2+√3)β ,(∠BCE = 45º-x)
tan(45º-x) = 1/(2+√3)
황갈색(45º-x) = (2-√3) = tan15º
(45º-x) = 15º
∴x = 30º
(TMI)
tan(AB) = (tanA – tanB) / {1+(tanA x tanB)} (삼각 항등식으로)
tan15º = tan(45º-30º) = (tan45º – tan30º) / {1+(tan45º x tan30º)}
tan15º = 1-(1/√3) / {1+(1/√3)}
tan15º = (√3-1) / (√3+1)
tan15º = (√3-1)² / 2
tan15º = (4-2√3) / 2
tan15º = (2-√3)